dgMARK: Decoding-Guided Watermarking for Diffusion Language Models

Pyo Min Hong¹, Albert No²,

¹Hongik University ²Yonsei University

TL;DR: Watermark text from diffusion LLMs by steering decoding order, not token probabilities,
achieving robust and low-distortion provenance.

dgMARK embeds a watermark by guiding which positions are unmasked, without altering token probabilities.

Introduction

We propose dgMARK, a decoding-guided watermarking method for discrete diffusion language models (dLLMs). Unlike autoregressive models, dLLMs can generate tokens in arbitrary order. While an ideal conditional predictor would be invariant to this order, practical dLLMs exhibit strong sensitivity to the unmasking order, creating a new channel for watermarking.

dgMARK steers the unmasking order toward positions whose high-reward candidate tokens satisfy a simple parity constraint induced by a binary hash, without explicitly reweighting the model's learned probabilities. The method is plug-and-play with common decoding strategies (e.g., confidence, entropy, and margin-based ordering) and can be strengthened with a one-step lookahead variant.

Watermarks are detected via elevated parity-matching statistics, and a sliding-window detector ensures robustness under post-editing operations including insertion, deletion, substitution, and paraphrasing.

Watermarking beyond left-to-right generation

discrete diffusion language models (dLLMs) have emerged as a strong alternative to the autoregressive paradigm. dLLMs iteratively denoise masked sequences and can finalize tokens in arbitrary order, supporting adaptive decoding strategies and controllable generation.

This order-agnostic decoding both creates challenges and opens new opportunities for watermarking. Here, We exploit the decoding order itself as the primary watermarking channel.

Decoding-guided Watermarking for dLLMs

The illustration below contrasts three paradigms: existing watermarking schemes, generic dLLMs decoding, and decoding-guided watermarking.

Existing Watermarking Schemes. Existing autoregressive watermarking methods generate green/red token sets by hashing the prefix (previous tokens) and embed watermark signals by biasing the sampling distribution toward green tokens.
Generic dLLMs Decoding. In contrast, dLLMs do not strictly follow left-to-right generation; instead, they iteratively denoise masked sequences, prioritizing high reward (e.g., confidence) masked positions and finalizing tokens in a flexible order.
Decoding-guided Watermarking. dgMARK leverages these rewards and embeds watermark signals by prioritizing high reward tokens that satisfy the parity condition.

We summarize generic dLLM decoding and our decoding-guided watermarking in the following pseudocode.

Generic dLLMs Decoding

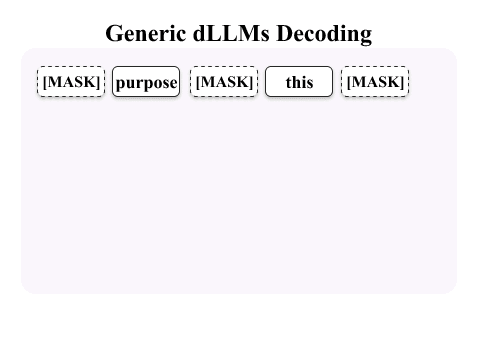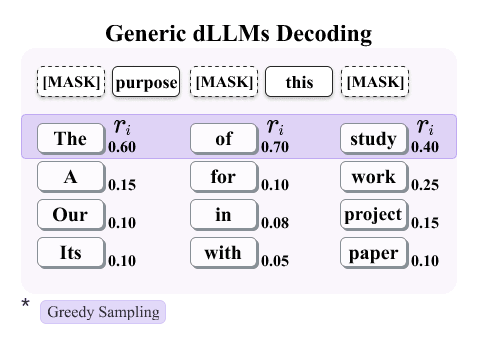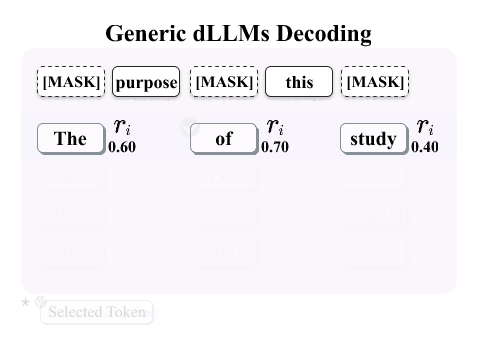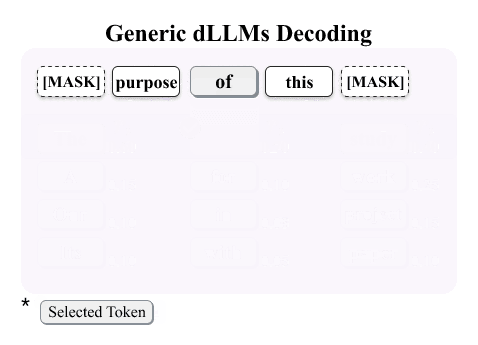
Require: Prompt $x$; output length $n$; predictor $p_\theta$; decoding strategy $\mathcal{F}$

$y \gets [\text{MASK}]^n$; $\mathcal{I} \gets \emptyset$
for $i = 1, \dots, n$ do
Get $\{(r_j, v_j) = \mathcal{F}(j; p_{\theta}, x, y_{\mathcal{I}})\mid j\notin\mathcal{I}\}$
$\mathcal{C} \gets \{ j \notin \mathcal{I} \}$
$k^\star \gets \arg\max_{j \in \mathcal{C}} r_j$
$y_{k^\star} \gets v_{k^\star}$ ; $\mathcal{I} \gets \mathcal{I} \cup \{k^\star\}$
end for
return $y$

dgMARK: Watermarks by Decoding

Require: Prompt $x$; output length $n$; predictor $p_\theta$; decoding strategy $\mathcal{F}$; parity matching set $\mathcal{G}_j$

$y \gets [\text{MASK}]^n$; $\mathcal{I} \gets \emptyset$
for $i = 1, \dots, n$ do
Get $\{(r_j, v_j) = \mathcal{F}(j; p_{\theta}, x, y_{\mathcal{I}})\mid j\notin\mathcal{I}\}$
$\mathcal{C} \gets \{ j \notin \mathcal{I} \mid v_j \in \mathcal{G}_j \}$
if $\mathcal{C} = \emptyset$ then $\mathcal{C} \gets \{\, j \notin \mathcal{I} \,\}$ end if
$k^\star \gets \arg\max_{j \in \mathcal{C}} r_j$
$y_{k^\star} \gets v_{k^\star}$; $\mathcal{I} \gets \mathcal{I} \cup \{k^\star\}$
end for
return $y$

Experimental Results

Watermark Detectability

Method	PPL $\downarrow$	FPR $\downarrow$	TNR $\uparrow$	TPR $\uparrow$	FNR $\downarrow$	TPR @ FPR $\uparrow$
Method	PPL $\downarrow$	FPR $\downarrow$	TNR $\uparrow$	TPR $\uparrow$	FNR $\downarrow$	10%	1%	0.1%	0.01%
Greedy Sampling	4.03
KGW ($\delta$ = 1)	4.33	0.0	1.0	0.072	0.928	88.52	62.68	30.14	11.48
KGW ($\delta$ = 2)	5.02	0.0	1.0	0.866	0.134	100.00	97.31	93.01	97.63
KGW ($\delta$ = 3)	5.83	0.0	1.0	0.970	0.030	100.00	100.00	98.52	97.78
PATTERN-MARK ($\delta$ = 1)	4.11	0.0	1.0	0.000	1.000	21.76	4.17	1.39	0.00
PATTERN-MARK ($\delta$ = 2)	4.72	0.0	1.0	0.040	0.960	73.50	48.50	20.50	12.00
PATTERN-MARK ($\delta$ = 3)	5.86	0.0	1.0	0.584	0.416	96.26	91.59	87.38	78.97
dgMARK	4.44	0.0	1.0	0.540	0.460	97.86	91.98	76.47	60.96
+ 3-beam	4.75	0.0	1.0	0.963	0.037	100.00	99.54	98.62	97.25
+ 5-beam	5.01	0.0	1.0	0.987	0.013	100.00	100.00	99.56	98.69
+ 8-beam	5.16	0.0	1.0	0.991	0.008	100.00	100.00	100.00	99.12
Multinomial Sampling	4.21
KGW ($\delta$ = 1)	5.59	0.0	1.0	0.107	0.893	89.80	60.91	32.99	14.21
KGW ($\delta$ = 2)	6.38	0.0	1.0	0.876	0.124	99.41	98.82	97.65	91.18
KGW ($\delta$ = 3)	7.87	0.0	1.0	0.984	0.016	100.0	99.21	99.21	98.41
PATTERN-MARK ($\delta$ = 1)	5.45	0.0	1.0	0.000	1.000	25.26	5.67	1.55	0.00
PATTERN-MARK ($\delta$ = 2)	6.33	0.0	1.0	0.060	0.940	78.00	53.50	27.50	16.50
PATTERN-MARK ($\delta$ = 3)	7.69	0.0	1.0	0.586	0.414	98.99	95.96	91.41	83.33
dgMARK	5.27	0.0	1.0	0.929	0.071	100.0	100.0	99.41	95.29
+ 3-beam	5.40	0.0	1.0	1.000	0.000	100.00	100.00	100.00	100.00
+ 5-beam	5.76	0.0	1.0	1.000	0.000	100.00	100.00	100.00	100.00
+ 8-beam	6.00	0.0	1.0	1.000	0.000	100.00	100.00	100.00	100.00

Table 1. Empirical results under greedy and multinomial sampling with LLaDA 1.5 on the C4 dataset, reporting perplexity (PPL) and detection metrics. Greedy and multinomial sampling represent the non-watermarked baselines.

Table 1 compares dgMARK with two probability-biasing baselines (KGW and PATTERN-MARK) under multiple watermark strengths $\delta \in \{1,2,3\}$. The main takeaway is that dgMARK provides strong detectability while better preserving text quality. In particular, dgMARK attains high detectability with 3-beam search, and detectability further improves with larger beam sizes, while its perplexity increase remains consistently smaller than that of the probability-biasing schemes.

Text Generation Quality

Model	Method	Greedy Sampling			Multinomial Sampling
Model	Method	MMLU (Acc $\uparrow$)	GSM8K (Acc $\uparrow$)	HumanEval (Pass@1 $\uparrow$)	MMLU (Acc $\uparrow$)	GSM8K (Acc $\uparrow$)	HumanEval (Pass@1 $\uparrow$)
LLaDA	Non-watermarked	0.648	0.797	0.427	0.594	0.775	0.360
	KGW	0.558	0.662	0.092	0.520	0.464	0.055
	PATTERN-MARK	0.570	0.635	0.134	0.532	0.438	0.073
	dgMARK	0.647	0.787	0.280	0.588	0.735	0.226
	dgMARK +3-beam	0.647	0.771	0.268	0.580	0.678	0.152
LLaDA 1.5	Non-watermarked	0.650	0.821	0.400	0.601	0.808	0.348
	KGW	0.567	0.726	0.104	0.536	0.582	0.092
	PATTERN-MARK	0.579	0.670	0.152	0.540	0.513	0.079
	dgMARK	0.649	0.814	0.317	0.596	0.759	0.201
	dgMARK +3-beam	0.649	0.774	0.207	0.588	0.723	0.134
Dream	Non-watermarked	0.700	0.800	0.427	0.630	0.789	0.420
	KGW	0.558	0.661	0.287	0.523	0.444	0.134
	PATTERN-MARK	0.594	0.652	0.335	0.551	0.639	0.287
	dgMARK	0.695	0.746	0.470	0.647	0.686	0.390
	dgMARK +3-beam	0.695	0.701	0.342	0.636	0.648	0.262

Table 2. Benchmark results. Results on multiple dLLMs under greedy and multinomial sampling, comparing non-watermarked generation, probability-biasing baselines, and dgMARK (with and without 3-beam search).

Table 2 reports benchmark results on MMLU, GSM8K, and HumanEval to measure downstream task performance under watermarking. We evaluate both greedy and multinomial sampling, comparing: (1) non-watermarked, (2) KGW, (3) PATTERN-MARK, (4) dgMARK, and (5) dgMARK with 3-beam search. Across benchmarks and sampling settings, dgMARK consistently preserves generation quality, exhibiting the smallest performance degradation compared to the probability-biasing schemes.

BibTeX

@article{hong2026dgmark,
      title={dgMARK: Decoding-Guided Watermarking for Diffusion Language Models}, 
      author={Pyo Min Hong and Albert No},
      journal={arXiv preprint arXiv:2601.22985},
      year={2026}